四元代数应用于CSIDH
[2025.2 阿里云ctf ohmyDH]
题目:
from ast import literal_eval
FLAG = "aliyunctf{REDACTED}"
ells = [*primes(3, 128), 163]
p = 4*prod(ells)-1
B = QuaternionAlgebra(-1, -p)
i,j,k = B.gens()
O0 = B.quaternion_order([1, i, (i+j)/2, (1+k)/2])
def action(O, priv):
for i,ell in zip(priv,ells):
for _ in range(abs(i)):
O = O.left_ideal([ell, j-sign(i)]).right_order()
ω = sum((O0*O).basis())
α = ω[0]+ω[2]*j
return B.quaternion_order((α*O*~α).basis())
priv_a = [randint(-5, 5) for _ in range(len(ells))]
priv_b = [randint(-5, 5) for _ in range(len(ells))]
O_start = action(O0, literal_eval(input("start:")))
Oa = action(O_start, priv_a)
Ob = action(O_start, priv_b)
alarm(60)
print("Oa:", Oa.basis())
print("Ob:", Ob.basis())
Os = [QQ(e) for e in input("Os: ").split()]
Oshare = B.quaternion_order([B(Os[i:i+4]) for i in range(0,len(Os),4)])
assert Oshare.isomorphism_to(action(Oa, priv_b))
print("🚩 Ohhhhh DH master!", FLAG)
思路:
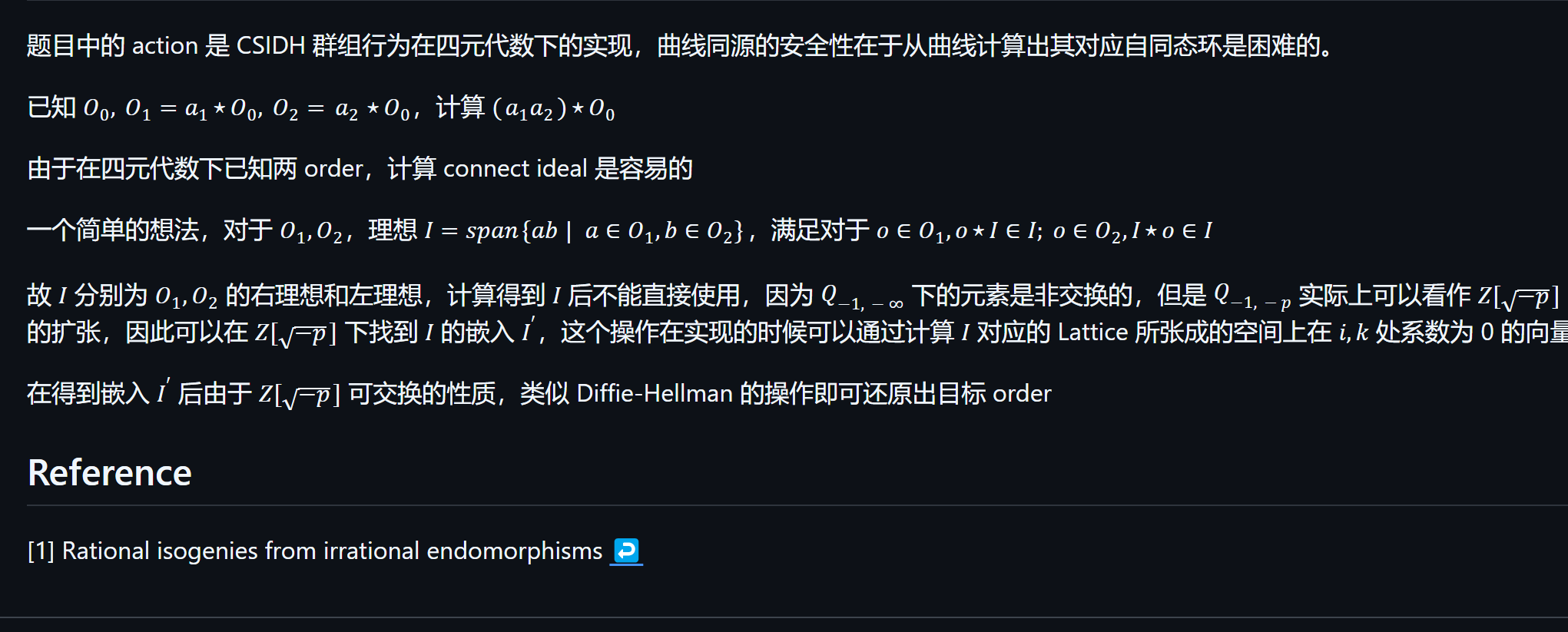
解题代码和解释:
ells = [*primes(3, 128), 163]
p = 4*prod(ells)-1
B = QuaternionAlgebra(-1, -p)
i,j,k = B.gens()
O0 = B.quaternion_order([1, i, (i+j)/2, (1+k)/2])
# Oa =
# Ob =
Oa = B.quaternion_order(Oa)
Ob = B.quaternion_order(Ob)
I = O0*Oa
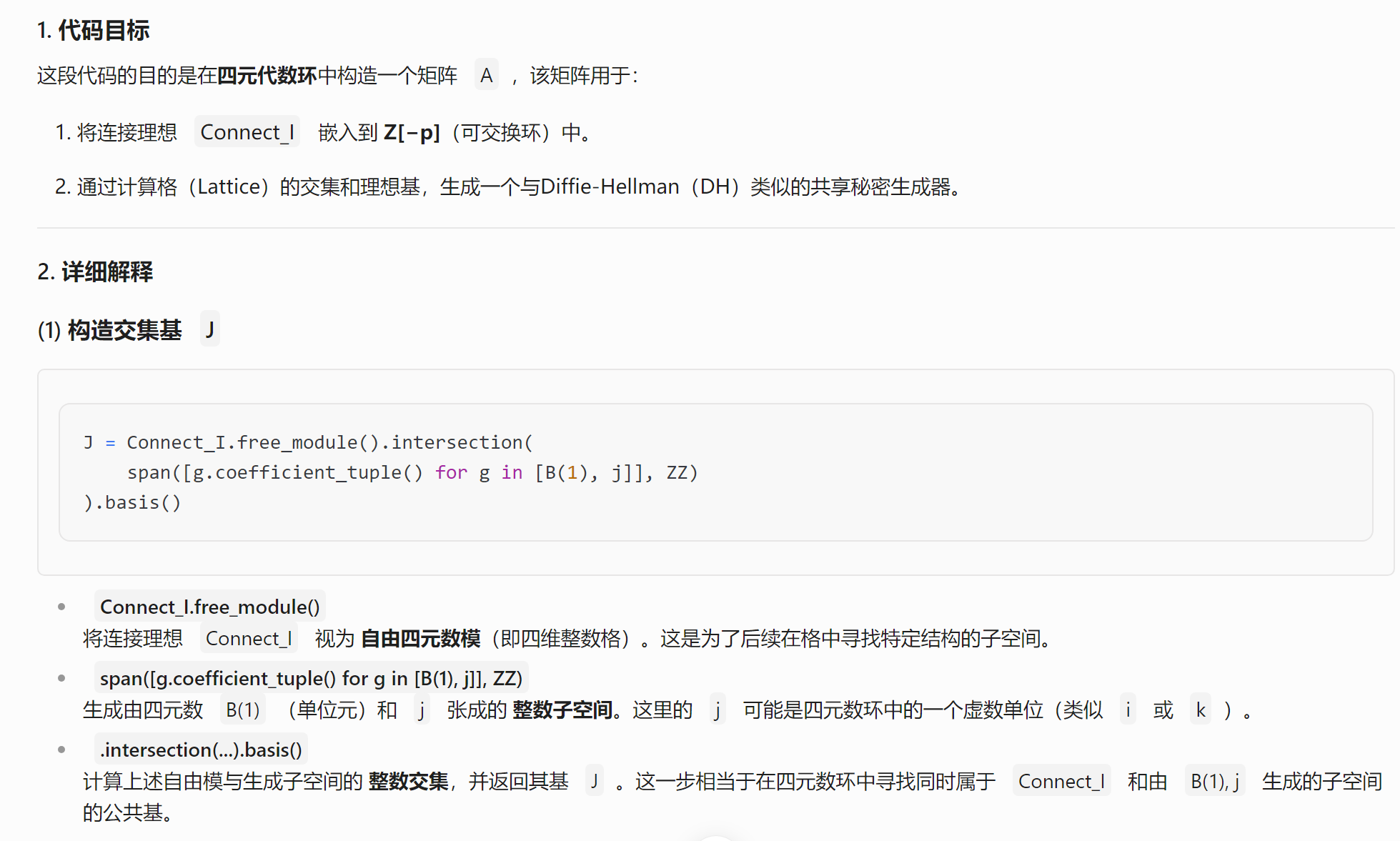
Connect_I = (1/I.norm())*I
J = Connect_I.free_module().intersection(span([g.coefficient_tuple() for g in [B(1), j]], ZZ)).basis()
A = matrix(QQ, [e.coefficient_tuple() for e in (Ob.left_ideal([B(j) for j in J]).right_order()).basis()])
print(str(A.list())[1:-1].replace(',',''))

free_module()的用法:

嵌入的意思:

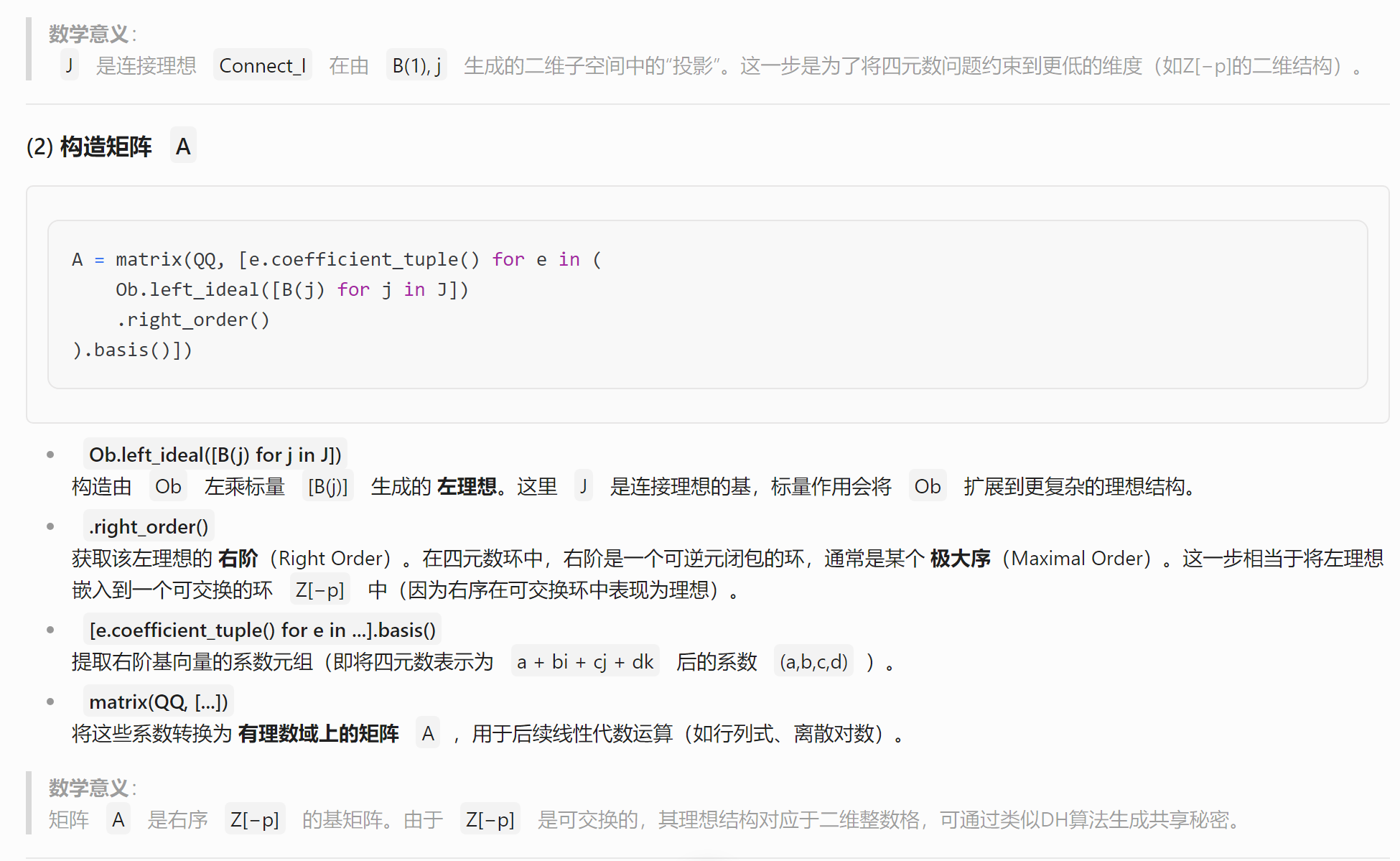
交换性与非交换性还是有很大区别的